Baseline Wander Removal dengan Wavelet

Pada post kali ini, kita akan melakukan proses menghilangkan baseline wander (baseline wander removal) pada sinyal EKG dengan menggunakan transformasi wavelet seperti yang ditulis oleh Sargolzaei et al pada paper dengan judul “A new robust wavelet based algorithm for baseline wandering cancellation in ECG signals“.

Latar belakang
Elektrokardiogram (EKG) adalah pembacaan sinyal elektrik jantung dengan cara menempelkan elektroda ke posisi tertentu pada tubuh dan kemudian membaca nilai perbedaan potensial listrik alias tegangan yang dihasilkan. Dari pembacaan ini kita bisa mencari tahu mengenai kondisi jantung. Akan tetapi, sinyal yang baru dibaca ini tidak lepas dari noise sehingga bisa mengganggu proses diagnosis. Sumber noise ini berasal dari berbagai macam, seperti elektroda dari elektroda itu sendiri atau jika tubuh bergerak ketika dilakukan pengukuran. Salah satu kondisi noise yang sering menyerang adalah situasi yang disebut baseline wander. Baseline wander terjadi apabila sinyal EKG tidak lurus pada sumbu x, malah naik turun. Contoh bisa dilihat di gambar 1.

Contoh sinyal yang terkena baseline wander dan hasilnya setelah dihilangkan. Gambar diambil tanpa izin dari paper yang dirujuk di atas.

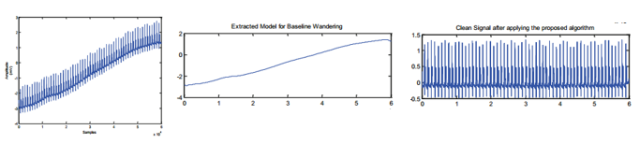
Baseline wander removal (BWR) adalah salah satu tahap preprocessing pada sinyal EKG untuk menghilangkan baseline drift ini. Ada beberapa teknik yang bisa dipakai, seperti melakukan filtering. Pada post ini, kita akan mengimplementasikan salah satu teknik yang memanfaatkan transformasi wavelet. Penjelasan dasar mengenai wavelet salah satunya bisa dilihat di http://users.rowan.edu/~polikar/WAVELETS/WTtutorial.html. Kelebihan dari teknik ini adalah kita tidak perlu menentukan parameter seperti ketika menggunakan high pass filter (frequency cut-off) sehingga metode kita bekerja secara non-supervised.

Sinyal EKG yang sudah bersih dari noise semacam ini kemudian bisa digunakan untuk berbagai macam kegunaan. Untuk pembahasan mengenai kegunaan sinyal EKG untuk mengenali tipe detak arrhythmia atau diagnosis tahapan tidur, bisa merujuk ke paper ini dan ini.

Algoritma
Berikut adalah tahapan dalam algoritma ini. Pertama, kita lakukan dekomposisi kepada sinyal asli dengan transformasi wavelet. Dalam hal ini kita memilih Daubechies orde 4 sebagai fungsi basisnya. Sinyal didekomposisi menjadi bagian frekuensi rendah/aproksimasi dan frekuensi tinggi/detail. Kemudian kita hitung nilai energi pada sinyal frekuensi tinggi. Kita cari kondisi dimana nilai energi pada level dekomposisi tersebut lebih rendah dari pada nilai pada level dekomposisi sebelumnya dan sesudahnya (alias lokal minima). Setelah kita temukan level tersebut, kita rekonstruksi sinyal aproksimasi dari level ini dengan membuang nilai pada sinyal frekuensi tinggi (atau dijadikan 0 semua). Sinyal hasil rekonstruksi ini kita sebut dengan baseline. Untuk menghilangkan baseline wander pada sinyal asli, maka kita kurangkan sinyal asli dengan sinyal baseline.

Gambar atas: plot nilai energi pada sinyal detail pada berbagai level dekomposisi. Tanda panah menunjukkan level ketika nilainya adalah lokal minima. Gambar bawah: Sinyal asli, baseline, dan sinyal asli yang sudah dikurang baseline. Lagi-lagi diambil dari paper rujukan di atas.

 

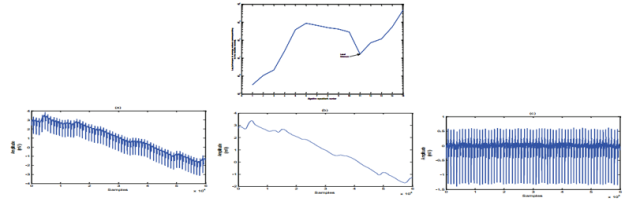
Implementasi
Pertama, kita implementasi metode konvolusi antara dua sinyal.

def conv(x, h):
    """ Perform the convolution operation between two input signals. The output signal length
    is the sum of the lenght of both input signal minus 1."""
    length = len(x) + len(h) - 1
    y = [0]*length

    for i in xrange(len(y)):
        for j in xrange(len(h)):
            if i-j >= 0 and i-j < len(x):
                y[i] += h[j] * x[i-j]

    return y

Lalu kita implementasi metode dekomposisi wavelet dan jangan lupa deklarasi koefisien basis fungsi yang dipakai. Dalam kasus ini adalah Daubechies dengan 4 koefisien. Dekomposisi dilakukan dengan cara mengkonvolusi sinyal asli dengan koefisien low pass and high pass. Sinyal keluaran dari proses ini kemudian di-downsampling menjadi setengahnya dengan cara hanya mengambil nilai pada posisi ganjil atau genap saja. Hal ini dilakukan berulang terhadap sinyal keluaran low pass (atau disebut aproksimasi) sebanyak parameter level.

c0 = (1+sqrt(3))/(4*sqrt(2))
c1 = (3+sqrt(3))/(4*sqrt(2))
c2 = (3-sqrt(3))/(4*sqrt(2))
c3 = (1-sqrt(3))/(4*sqrt(2))

def db4_dec(x, level):
""" Perform the wavelet decomposition to signal x with Daubechies order 4 basis function as many as specified level"""

    # Decomposition coefficient for low pass and high pass
    lpk = [c0, c1, c2, c3]
    hpk = [c3, -c2, c1, -c0]

    result = [[]]*(level+1)
    x_temp = x[:]
    for i in xrange(level):
        lp = conv(x_temp, lpk)
        hp = conv(x_temp, hpk)

        # Downsample both output by half
        lp_ds=[0]*(len(lp)/2)
        hp_ds=[0]*(len(hp)/2)
        for j in xrange(len(lp_ds)):
            lp_ds[j] = lp[2*j+1]
            hp_ds[j] = hp[2*j+1]

        result[level-i] = hp_ds
        x_temp = lp_ds[:]

    result[0] = lp_ds
    return result

Fungsi rekontruksi digunakan untuk mencari baseline dari sinyal asal. Rekonstruksi bekerja dengan melakukan konvolusi dengan koefisien rekonstruksi pada kedua sinyal low pass dan high pass, melakukan upsampling dengan menyelipkan 0 di setiap nilai pada sinyal dan kemudian masing-masing posisi pada sinyal saling dijumlahkan.

def db4_rec(signals, level):
    """ Perform reconstruction from a set of decomposed low pass and high pass signals as deep as specified level"""

    # Reconstruction coefficient
    lpk = [c3, c2, c1, c0]
    hpk = [-c0, c1, -c2, c3]

    cp_sig = signals[:]
    for i in xrange(level):
        lp = cp_sig[0]
        hp = cp_sig[1]

        # Verify new length
        length = 0
        if len(lp) > len(hp):
            length = 2*len(hp)
        else:
            length = 2*len(lp)

        # Upsampling by 2
        lpu = [0]*(length+1)
        hpu = [0]*(length+1)
        index = 0
        for j in xrange(length+1):
            if j%2 != 0:
                lpu[j] = lp[index]
                hpu[j] = hp[index]
                index += 1

        # Convolve with reconstruction coefficient
        lpc = conv(lpu, lpk)
        hpc = conv(hpu, hpk)

        # Truncate the convolved output by the length of filter kernel minus 1 at both end of the signal
        lpt = lpc[3:-3]
        hpt = hpc[3:-3]

        # Add both signals
        org = [0]*len(lpt)
        for j in xrange(len(org)):
            org[j] = lpt[j] + hpt[j]

        if len(cp_sig) > 2:
            cp_sig = [org]+cp_sig[2:]
        else:
            cp_sig = [org]

    return cp_sig[0]

Method calcEnergy menghitung nilai energi dari sebuah sinyal berdasarkan definisinya yaitu jumlahan kuadrat sinyal di tiap titik

def calcEnergy(x):
    """ Calculate the energy of a signal which is the sum of square of each points in the signal."""
    total = 0
    for i in x:
        total += i*i
    return total

Kemudian method bwr berikut adalah implementasi dari algoritma yang dijabarkan di atas.

def bwr(raw):
    """ Perform the baseline wander removal process against signal raw. The output of this method is signal with correct baseline
    and its baseline """
    en0 = 0
    en1 = 0
    en2 = 0
    n = 0

    curlp = raw[:]
    num_dec = 0
    last_lp = []
    while True:
        print 'Iterasi ke' + str(num_dec+1)
        print len(curlp)

        # Decompose 1 level
        [lp, hp] = db4_dec(curlp,1)

        # Shift and calculate the energy of detail/high pass coefficient
        en0 = en1
        en1 = en2
        en2 = calcEnergy(hp)
        print en2

        # Check if we are in the local minimum of energy function of high-pass signal
        if en0 > en1 and en1 < en2:
            last_lp = curlp
            break

        curlp = lp[:]
        num_dec = num_dec+1

    # Reconstruct the baseline from this level low pass signal up to the original length
    base = last_lp[:]
    for i in xrange(num_dec):
        base = db4_rec([base,[0]*len(base)], 1)

    # Correct the original signal by subtract it with its baseline
    ecg_out = [0]*len(raw)
    for i in xrange(len(raw)):
        ecg_out[i] =  raw[i] - base[i]

    return (base, ecg_out)

Contoh
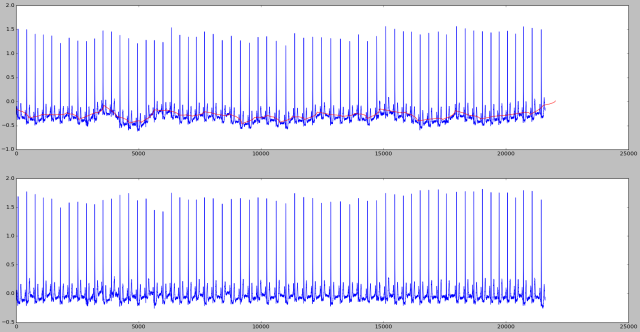
Untuk contoh kita ambil data dari situs Physionet khususnya MIT-BIH Arrhythmia database. Data diambil dari salah satu record pasien dengan kode nomor 101. Sinyal EKG diambil sepanjang 1 menit. Sinyal EKG yang diambil berasal dari lead II dan V5.

Contoh kode untuk memanggil modul dan fungsi yang sudah dibuat di atas adalah sebagai berikut

import bwr
import matplotlib.pyplot as plt

# Read input csv file from physionet
f = open('samples1.csv', 'r')
lines = f.readlines()
f.close()

# Discard the first two lines because of header. Takes either column 1 or 2 from each lines (different signal lead)
signal = [0]*(len(lines)-2)
for i in xrange(len(signal)):
	signal[i] = float(lines[i+2].split(',')[1])

# Call the BWR method
(baseline, ecg_out) = bwr.bwr(signal)

plt.subplot(2,1,1)
plt.plot(signal, 'b-')
plt.plot(baseline, 'r-')

plt.subplot(2,1,2)
plt.plot(ecg_out, 'b-')
plt.show()

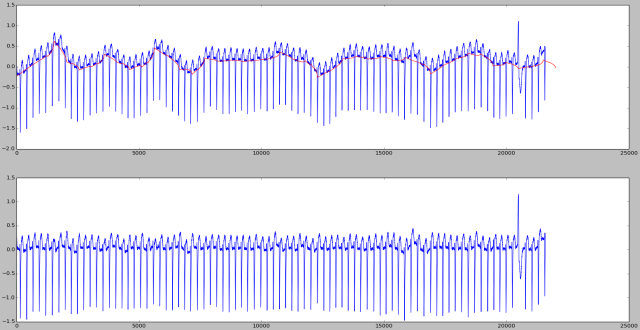
Berikut contoh pertama. Garis merah pada plot merupakan baseline dari sinyal EKG.

Berikut adalah contoh kedua.

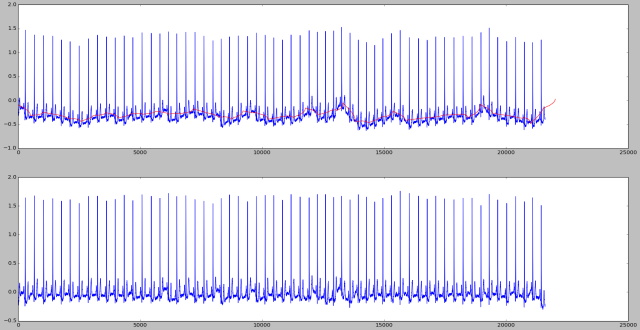
Contoh berikut diambil dari lead V5.

Kode lengkap dan sampel sinyal dapat dilihat di: https://github.com/mitbal/py-bwr

Semoga berguna. Salam.